Фигура технического анализа треугольник: нисходящий, восходящий, симметричный

Равносторонний треугольник (понятие, определение):

Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.

Равносторонний треугольник называется также правильным или равноугольным треугольником.

По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.

Рис. 1. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

Описание треугольников

Начиная писать любую статью, хочется сделать ее, прежде всего уникальной и неповторимой. Подписчики моего сайта, должны находить ответы на все свои вопросы в моих статьях. По этой причине, приходится перечитывать кучу литературы и статей с аналогичных моему сайтов.

В итоге оказывается, создать уникальную статью совсем не сложно. К сожалению, практически все владельцы форекс сайтов, скачивают информацию друг у друга, и практически все статьи как под копирку. Конечно это возмущает, не уж то нет своей головы, но да ладно, вернемся к теме.

Практически во всех книгах, и на всех сайтах, трейдеры сходятся во мнении, что фигура графического анализа треугольник — фигура неопределенности. И хотя ее классифицируют, как фигуру продолжения тренда, не всегда это срабатывает.

Виды треугольников

Всего имеется 4 вида треугольников, одна из них разворотная фигура, и три фигуры продолжения тренда. Надо понимать, что все это условно и к каждой сделке, нужно подходить индивидуально.

К разворотным фигурам, относится:

расходящийся треугольник.

К фигурам продолжения, относятся:

• симметричный треугольник;
• нисходящий треугольник;
• восходящий треугольник.

Построение треугольника

Построить любой из выше перечисленных треугольников, можно всего лишь по 4 точками.

По такому же принципу, строятся и остальные виды треугольников. В случае симметричного, нисходящего и восходящего треугольников, обязательное правило, линии должны сходились, для расширяющегося треугольника, расходились.

Пробой треугольника

В различных книгах по техническому анализу пишут: «Выход из треугольника, в большинстве случаев будет противоположный от входа». Это значит, если до начала формирования треугольника, тренд был вверх, то и выход из треугольника будет вверх (исключение, расходящийся треугольник). Но, в тех же книгах по трейдингу, встречаются фразы по типу: «Нельзя заранее определить в какую сторону будет выход». 

Поэтому предлагаю не гадать, а использовать единственно верный метод, дождаться выхода (пробоя) и следовать за ценой.

Если мы видим, что цену зажимают в фигуру технического анализа Треугольник, то чего нам торопиться? Цена никуда не убежит, есть время подождать. А вот когда произойдет пробой треугольника, это наш сигнал в какую сторону собирается двигаться рынок. Здесь то и можно вступать в игру. Входим на ретесте пробитого уровня, и торгуем по тренуд.

Где ставить take profit? 

Не решенным остался только один вопрос, где ставить take profit? 

Для расчета профита, нужно отложить максимальную ширину треугольника, от места пробой. Заложитесь на несколько пунктов в меньшую сторону и ждать тейка.

Элементы тупоугольного треугольника:

Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.

Рис. 5. Тупоугольный треугольник и внешний угол

∠ ВAD – острый угол

Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника

MA – медиана тупоугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника

MС – высота тупоугольного треугольника

Высота тупоугольного треугольника может лежать за пределами треугольника.

Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника

MA – биссектриса тупого угла тупоугольного треугольника

Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Виды треугольников

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

• остроугольные
• прямоугольные
• тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

• равносторонние
• равнобедренные
• разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

разносторонний треугольник

равносторонний треугольник

равнобедренный треугольник

Задачи и решения

Задача 1. На сторонах угла CAD отмечены точки B и E так, что точка B лежит на отрезке AC, а точка E − на отрезке AD, причем AC=AD и AB=AE. Докажите, что ∠CBD=∠DEC (Рис.9).

Доказательство. AC=AD, AE=AB, ∠CAD общий для треугольников CAE и DAB. Тогда, по первому признаку равенства треугольников (теорема 1) ⊿ACE=⊿ADB. Следовательно ∠DBA=∠AEC. Поскольку углы CBD и DBA смежные, то CBD=180°−∠DBA. Аналогично CED=180°-∠AEC. То есть ∠CBD=∠DEC. Конец доказательства.

Задача 2. По данным рисунка рис.10 докажите, что OP=OT, ∠P=∠T

Доказательство. OC=OB, ∠TCO=∠PBO=90°. Углы TOC и POB вертикальные (следовательно равны) тогда, повторому признаку равенства треугольников (теорема 2), ⊿TCO=⊿PBO. Конец доказательства.

[править] См. также

По числу вершин	1-10 Одноугольник • Двуугольник • Треугольник • Четырёхугольник (Дельтоид) • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Десятиугольник 11-20 Одиннадцатиугольник (англ.) • Двенадцатиугольник • Тринадцатиугольник • Четырнадцатиугольник
Правильные	Выпуклые Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • … • 17-угольник • … • 257-угольник • … • 65537-угольник Звёздчатая форма Звезды (Пентаграмма • Гексаграмма • Октаграмма)
Выпуклые	Четырёхугольники: Параллелограмм • Прямоугольник • Ромб • Трапеция
Невыпуклые	Контрпараллелограмм
Теория и практика	Принадлежность точки многоугольнику • Теорема Бойяи — Гервина • Теорема Брахмагупты • Теорема Гаусса — Ванцеля • Формула Пика • Теорема о сумме углов многоугольника

Первый признак равенства треугольников

Теорема 1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁C₁ (Рис.3). Пусть AB=A₁B₁, AС=A₁С₁ и ∠A=∠A₁. Докажем, что .

Так как ∠A=∠A₁, то треугольник ABC можно наложить на треугольник A₁B₁C₁ так, чтобы вершины A и A₁ совпадали, а стороны AB и AС наложились на лучи A₁B₁ и A₁C₁, соответственно.

Так как по условию теоремы AB=A₁B₁, AС=A₁С₁, то сторона AB совместится со стороной A₁B₁, а сторона AС − со стороной A₁С₁.Тогда совместятся B и B₁, C и С₁. Следовательно сторона BC совместится со стороной B₁C₁. То есть треугольники ABC и A₁B₁C₁ полностью совместятся. Теорема доказана.

Формулы равностороннего треугольника:

Пусть a – длина стороны равностороннего треугольника, h – высота (l – биссектриса, m – медиана) равностороннего треугольника, проведенная к каждой стороне, α – угол равностороннего треугольника, α = 60°, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6).

Рис. 6. Равносторонний треугольник

Формула радиуса вписанной окружности (r):

 .

Формула радиуса описанной окружности (R): 

,

.

Формулы периметра (Р) равностороннего треугольника: 

.

Формулы площади (S) равностороннего треугольника: 

 .

Формулы высоты (h), медианы (m) и биссектрисы (l) треугольника:

.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
9 631

Точка пересечения высот треугольника

Теорема 6

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что ${CC}_1\bot A_2B_2,\ {BB}_1\bot A_2C_2,\ {AA}_1\bot C_2B_2$. Следовательно, ${AA}_1,\ {BB}_1,\ {CC}_1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты ${AA}_1,\ {BB}_1,\ {CC}_1$ пересекаются в одной точке.

Теорема доказана.

Какие бывают геометрические фигуры?

Какие бывают геометрические фигуры?

• В сферу изучения науки геометрии входят плоские (двухмерные) фигуры и объмные фигуры (трхмерные).

  Из плоских:

  Их изучает планиметрия. Точка тоже плоская фигура.

  Из объмных известны:

  Их изучает стереометрия.

• К фигурам также относится и точка.

  Трехмерные фигуры — куб, сфера, полусфера, конус, цилиндр, пирамида, параллелепипед, призма, эллипсоид, купол, тетраэдры и множество других, выходящие из вышеуказанных. Далее идут очень сложные геометрические фигуры — различные многогранники, которые по сути могут содержать бесконечное количество граней. Например, большая клинокорона — состоит из 2-х квадратов и 16-ти правильных треугольников или клинокорона, составленная из 14 граней: 2 квадрата и 12 правильных треугольника.

• Говоря о геометрических фигурах, можно выделить такие две закономерные группы как:

  1) Двухмерные фигуры;

  2) И трхмерные фигуры.

  Итак, поподробнее о двухмерным, к ним можно отнести такие фигуры как:

  А вот что касается трхмерных фигур, то вот какими они могут быть:

• Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры). Я в школе любила и ту, и другую науку.

  Вот так классифицируются плоские (2D) фигуры:

  **

  Объемные фигуры (3D) классифицируются таким образом:

  **

  Это куб, параллелепипед, тетраэдр, цилиндр, пирамида, икосаэдр, шар, додекаэдр, конус, октаэдр, призма, сфера. К тому же есть усеченные фигуры (пирамида, конус). В зависимости от основания, пирамида, призма делятся на треугольные, четырехгранные и так далее.

  Детские игрушки (пирамидки, мозаика и другие) позволяют с раннего детства знакомить детей с геометрическими объемными фигурами. А плоские фигуры можно нарисовать и вырезать из бумаги.

• Из двухмерных можно назвать следующие:

  • круг;
  • овал;
  • квадрат;
  • прямоугольник;
  • параллелограмм;
  • трапеция;
  • пятиугольник (шестиугольник и т.д.);
  • ромб;
  • треугольник.

  С трехмерными немного посложнее:

  • куб;
  • цилиндр;
  • конус;
  • призма;
  • сфера или шар;
  • параллелепипед;
  • пирамида;
  • тетраэдр;
  • икосаэдр;
  • октаэдр;
  • додекаэдр.

  Думаю многие, прочитав последния названия, спросили про себя: quot;Что-что?quot;. Для наглядности — иллюстрация:

• На самом деле фигур в математике достаточно. Плоские фигуры это — прямоугольники, квадрат, треугольник, пятиугольник, шестиугольник, круг. Объемные фигуры или 3D фигуры — это как пирамида, так и куб и додекаэдр, и тд.

• 1 Из двухмерных фигур:

  2 Из трхмерных фигур:

  Призма, пирамида, параллелепипед, призма, шар (сфера), цилиндр, полусфера (половинка от сферы, то есть шар, разрезанный пополам) и конус. Пирамиды делятся на треугольные, четырхугольные и так далее (почти до бесконечности). Чем больше у пирамиды углов в основании, тем больше она напоминает конус.

• Трхмерные фигуры (3D): двугранный угол, многогранный угол; многогранник (разновидности многогранников: призма разновидности призмы: параллелепипед, куб, антипризма, пирамида разновидность тетраэдр, усечнная пирамида, бипирамида разновидность октаэдр, додекаэдр, икосаэдр, клин, обелиск); цилиндр, усечнный цилиндр, отрезок цилиндра (он же цилиндрическая подковка или quot;копытоquot;), конус, усечнный конус, сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор, эллипсоид, геоид…

• С самого начала мы на уроках геометрии изучаем простые фигуры, которые являются плоскими, то есть располагаются на одной плоскости.

  Далее, перед нами открывается мир объмных фигур, которые необходимо представлять и понимать, как они расположены и как грамотно их нарисовать, чтобы было понятно не только вам, но и окружающим.

  Итак, перечень основных фигур можно изучить ниже.

• В последнее время мне как раз приходилось рассказывать своим внучкам и внуку, какими могут быть геометрические фигуры.

  Начинали с плоских фигурок, вырезанных из картона или сделанные из пластмассы, дети учились различать треугольник и квадрат, овал и круг, прямоугольник, ромб и многоугольник.

  Помогали в запоминании названий фигур и вот такие специальные игрушки с отверстиями определнной формы.

  Позднее перешли на объмные фигурки, кубики и конусы, параллелепипеды, шары и кольца, пирамидки и цилиндры.

  До школы они пока не доросли, а когда пойдут, то их научат различать равнобедренные и равносторонние треугольники, узнают про луч и точку, про окружность и вс остальное.

Названия геометрических фигур в картинках (23 ФОТО)

Геометрия как наука началась с древних греков. Они подстмотрели у египтян землемерные работы и оформили это в виде аксиом и правил. Первым научным трудом в этой области был «Начала» Евклида.

Объёмные геометрические фигуры

Разноцветные фигуры

Названия объёмных фигур на английском

Синие фигуры с английскими названиями

Синие фигуры с русскими названиями

Разноцветные фигуры с английскими названиями

Простые фигуры кубической сингонии

Куб, икосаэдр, тетраэдр, октаэдр, додекаэдр

Весёлые геометрические фигуры

Shapes

Конус

Треугольник, пятиугольник, шестиугольник, семиугольник, восьмиугольник

Ромб

Призмы

Пирамиды

Третий признак равенства треугольников

Теорема 3. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁. Пусть AB=A₁B₁, AC=A₁C₁ и BC=B₁C₁. Докажем, что . Приложим треугольник ABC к треугольнику A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, вершина B совмещалась с вершиной B₁, а вершины С и С₁ находились по разные стороны от прямой A₁B₁.

Возможны три варианта: луч CC₁ проходит внутри угла ACB(Рис.6); луч CC₁ совпадает с одной из сторон угла ACB (Рис.7); луч CC₁ проходит вне угла ACB(Рис.8). Рассмотрим эти три случая по отдельности.

Вариант 1 (Рис.6). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и ∠3=∠4 и, следовательно:

Имеем AC=A₁C₁, BC=B₁C₁ ∠ACB=∠A₁C₁B₁ и по первому признаку равенства треугольников . Теорема доказана.

Вариант 2 (Рис.7). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольник BСС₁ равнобедренный. Тогда ∠1=∠2. Имеем: AC=A₁C₁, BC=B₁C₁, ∠1=∠2 и по первому признаку равенства треугольников . Теорема доказана.

Вариант 3 (Рис.8). Так как по условию теоремы AC=A₁C₁ и BC=B₁C₁, то треугольники AСС₁ и BСС₁ равнобедренные. Тогда ∠1=∠2 и и, следовательно:

Имеем AC=A₁C₁, BC=B₁C₁ и по первому признаку равенства треугольников . Теорема доказана.

Происхождение

Сказать точно, когда и где появился первый музыкальный треугольник, к сожалению, пока что нельзя. На данный момент известно только то, что первые модели этого инструмента создавались в виде трапеции и выглядели как стремя Средних веков. Выяснено это благодаря работам некоторых английских и итальянских художников, которые и изобразили данный инструмент в некоторых своих работах.

Первое упоминание о подобном треугольнике можно встретить только в вюртембергской имущественной описи, которая датируется 1389 годом. Но согласно некоторым сведениям, скорее всего, данный инструмент появился в восточных районах, а конкретно в Турции. Самое первое упоминание о нём датируется пятнадцатым столетием.

Нельзя сказать точно и о том, в какой именно период инструмент приобрёл свою треугольную форму, которая является для нас наиболее привычной, но уже к семнадцатому столетию он имел три разновидности, а потом и пять.

В России треугольник «заявил» о себе приблизительно в 1775 году. Он быстро обрёл популярность и востребованность из-за колорита, который был довольно экзотичным и напоминал о Востоке.

Одной из первых опер, в которой можно было услышать звучание музыкального треугольника, стала опера французского композитора Андре Гретри под названием «Тайная магия», однако в оркестрах с военными музыкальными композициями он стал использоваться значительно раньше. Известно, что треугольник был востребован в войсках во время правления императрицы Елизаветы Петровны.

Этот инструмент использовали и другие известные музыкальные классики, в числе которых композитор Йозеф Гайден, Вольфганг Амадей Моцарт, а также Людвиг ван Бетховен, Иоганн Штраус и Николай Андреевич Римский-Корсаков. В их творчестве этот инструмент был наиболее часто задействован для того, чтобы создать образы, связанные с Востоком, а также обогатить палитру звуков своих музыкальных композиций.

Из всех произведений, где у музыкального треугольника есть своя собственная партия, наиболее знаменитым является первый концерт для фортепиано с оркестром Ференца Листа, который прошел в 1849 году. Многие в качестве шутки стали называть его концертом для треугольника, ведь этот инструмент в данном произведении не только выполняет роль фона, но и полностью отвечает за одну из партий, открывая тем самым третью часть концерта под названием «Allegretto vivace».

В нынешнее время столь интересный музыкальный инструмент всё ещё не утратил свою значимость в сфере музыки. Без него трудно представить современный оркестр, ведь именно он оживляет его звучание, придаёт ему нотки торжественности и величия, а также делает его более богатым и насыщенным.

Большой популярностью в нынешнее время треугольник пользуется не только в оркестрах, но и в праздничное время в Греции. Используют его как аккомпанемент в период Нового года и Рождества преимущественно дети во время колядок, поздравлений и песен. Звук этого инструмента создаёт атмосферу и настроение настоящего праздника и напоминает о сказке.

Свойства остроугольного треугольника:

Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 8. Остроугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 9. Остроугольный треугольник с равными боковыми сторонами

АВ = ВС

3. Сумма углов остроугольного треугольника равна 180°.

4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:

• • a < b + c;
  • a > b – c;
  • b < a + c,
  • b > a – c;
  • c < a + b;
  • c > a – b.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
1 792

Точка пересечения серединных перпендикуляров треугольника

Теорема 4

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

Пусть дан треугольник $ABC$, $n,\ m,\ p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n\ и\ m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Теорема 5

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC,\ OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Теорема доказана.

Третий признак равенства треугольников

Теорема:

Два треугольника равны, если три стороны одного треугольника равны трём сторонам другого.

Доказательство:

Рассмотрим два треугольника  ABC  и  A₁B₁C₁,  у которых:

AB = A₁B₁,  BC = B₁C₁,  AC = A₁C₁.

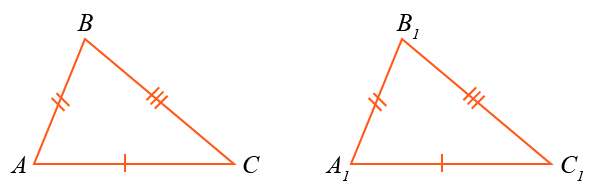
Требуется доказать, что

ABC = A₁B₁C₁.

Приложим треугольники  ABC  и  A₁B₁C₁  один к другому так, чтобы вершина  A  совместилась с  A₁,  вершина  C  — с  C₁, а вершины  B  и  B₁  оказались по разные стороны от прямой  AC.

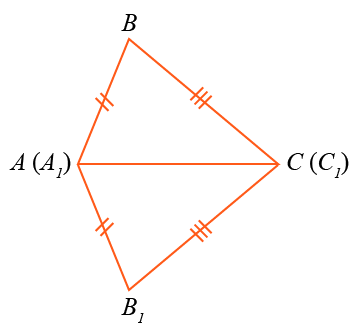
Соединив точки  B  и  B₁,  получим два равнобедренных треугольника  BAB₁  и  BСB₁.

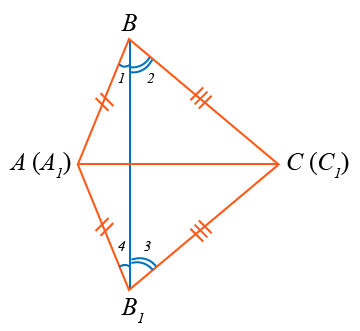
В треугольнике  BAB₁  ∠1 = ∠4,  в  BСB₁  ∠2 = ∠3  (как углы при основании). Следовательно,

∠1 + ∠2 = ∠4 + ∠3,  поэтому  ∠ABC = ∠AB₁C.

Итак,  AB = A₁B₁,  BC = B₁C₁,  ∠ABC = ∠A₁B₁C₁.

Из этого следует, что треугольники  ABC  и  A₁B₁C₁  равны по первому признаку равенства треугольников. Теорема доказана.

Внешний вид

Интересным является тот факт, что в рунических в символах Валькнут встречается изображенным по-разному:

• В первой версии – это переплетение 3 отдельных треугольников, образующих собой единую цепь.
• Вторая – это единая непрерывная линия, не имеющая ни начала, ни конца, выложенная таким образом, что при пересечении самой себя она формирует ломаную выложенную треугольниками.

Валькнут

Сейчас нет единого мнения об однозначности трактовки данного символа. К тому же 2 образа совершенно по-разному расшифровываются:

• Тот, что представляет собой 3 независимые фигуры, сложенные вместе, рассматривается как власть верховного Бога над невидимыми связями и цепями в этом мире. Только Одину подвластно запутать человека, связав его действия, поступки и чувства страхом или предубеждениями. Так же как ему одному по силам разрубить все сомнения и предоставить возможность развиваться и двигаться вперед каждой личности.
• Рассматривая рун, состоящий из одной сплошной линии, которая переплетается в 3 образа треугольника, стоит отметить, что его вообще считают символом судьбы. Это символ того, что норны, прядя одну единую нить судьбы каждого человека, условно разделяют ее на 3 вехи – настоящее, прошлое и будущее.

Точка пересечения медиан треугольника

Теорема 1

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

Рассмотрим треугольник $ABC$, где ${AA}_1,\ {BB}_1,\ {CC}_1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $\angle ABB_1=\angle BB_1A_1,\ \angle BAA_1=\angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Теорема доказана.

Валькнут в руническом круге

Как было сказано выше, руны, расположенные вокруг валькнута, могут менять его значение.

Как правило, этот символ и изображается в окружении рун. Обычно это Дагаз, Турисаз, Уруз и Феху.

Данные руны циклично повторяются, что символизирует прибавление опыта со временем, а также развитие при постоянном продвижении.

При этом положение знака по отношению к руническим символам может иметь 8 вариантов (вариант определяется в зависимости от тех рун, на которые указывают выступающие углы валькнута), отчего изменяется значение оберега валькнут.

Вот смысл рун, в круг которых заключается рассматриваемый знак:

• Феху – обозначает материальное начало. На
  материальном базируется построение дальнейшего опыта;
• Уруз – энергия преодоления препятствий.
  Позволяет идти дальше на пути к познанию;
• Турисаз – защищает на избранном пути;
• Дааз или Дагаз – завершает начинание. Это руна
  перехода в новое состояние, символизирует перемены.

Руны в кругу повторяются, что символизирует непрерывный
жизненный цикл и постоянное самосовершенствование носителя.

Числовой символизм валькнута

Числа играют очень важную роль во всех языческих религиях. Числовой символизм, соответственно, присущ и скандинавскому язычеству.

Числа, отраженные в изображении «узла павших» — это 3 и 9. Они имеют свое собственные сакральное значение. 9 – это число миров в скандинавской мифологии:

1. Мир богов или Асгард.
2. Мир людей или Мидгард.
3. Мир умерших или Хельхейм.
4. Мир ванов или Ванахейм.
5. Мир великанов или Йотунхейм.
6. Мир светлых альвов или Альвхейм.
7. Мир огненных великанов или Муспельхейм.
8. Мир ледяных великанов или Нифльхейм.
9. Мир карликов или Свартальфахейм.

Также 9 – число ветвей мирового ясеня Иггдрассиля (по одному
на каждый мир). 9 ветвей – основа рун старшего алфавита (футарка). 3 – число
норн (богинь судьбы), отражающее настоящее, прошлое и будущее.

Почему фигура технического анализа Треугольник вообще появляется?

Перечитывая в очередной раз представленный материал на других сайта и в различных книгах, пришел к выводу, что люди, составляющие описание фигуре Треугольник (все равно какой), не до конца понимаю, что происходит на рынке в самом деле.

Многие пишут: «Рынок ослаб и поэтому появился треугольник». Да ничего подобного. Маркет мейкер запутал трейдера так, что тот не понимает куда торговать. То цена вверх, то вниз и трейдер новичок, пытаясь поймать движение, вместе с ценой и прыгает, да только входит в самом конце, когда рынок разворачивается. 

Значит на рынке не столько слабость, сколько паника. Трейдеры не понимаю как торговать, а крупному игроку надо всех затянуть в рынок, чтобы все деньги были в рынке.

Сам ловил себя на мысли: «Какая разница, понимаю я или нет, главное чтобы профит был», но все же, хочется объяснить свое видение появления фигур технического анализа Треугольник.

Нисходящий треугольник

Фигура технического анализа Нисходящий треугольник

На представленном рисунке, изображена фигура технического анализа нисходящий треугольник. В таком контексте, когда цена заходит в треугольник снизу, другими словами идет up тренд, пробой должен состояться вверх и будет все правильно и по закону.

Но, если бы был down тренд и появился нисходящий треугольник, то куда должна была бы пойти цена? По книжной логике, вниз, но понимая суть уровней поддержки / сопротивления, могу заявить, что это было бы не правильно.

Почему? Давайте объясню, дело в том, что у нисходящего треугольника, нижняя граница, ни что иное как уровень поддержки. В одной из статей описывал, что на столько ровные уровни, могут быть только в одном случае, когда крупный игрок заходит отложенными ордерами.

И что получается. Крупный игрок постоянно от нижней границе подкупает, набирая себе нужную позицию и упорно поддерживая данный уровень. Чего он ждет? Ну во первых, когда соберется позиция, а во вторых, когда ослабнут покупатели. В этот момент и состоится пробой вверх.

Восходящий треугольник

Фигура технического анализа Восходящий треугольник

Фигура противоположная нисходящему треугольнику. Думаю вам не составит труда определить логику этой модели. Как вы думаете, куда пойдет цена? Вверх? Нет, цена пойдет вниз.

Специально нарисовал предшествующий восходящему треугольнику тренд вверх. Да только в данной модели, верхняя граница треугольника, ни что иное, как уровень сопротивления. По аналогии с нисходящим треугольником, мы понимаем, что уровень держит крупный игрок и входит от него отложенными ордерами набирая позицию в шорт.

Симметричный треугольник

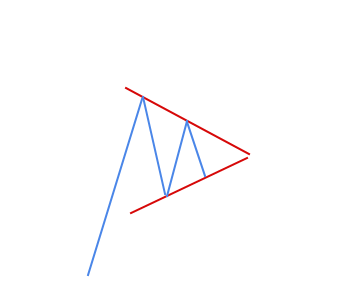
Фигура технического анализа Симметричный треугольник

С описанием симметричного треугольника, можно согласиться. Если до треугольника тренд был вверх, то и выход должен быть вверх. Ведь ничего не изменилось. Началу тренда предшествовал набор позиции, и чтобы изменить тренд, нужно позицию разгрузить, чего мы не видим.

В данном контексте, симметричный треугольник может говорить только об одном, крупный игрок добирает позицию.

Расходящийся треугольник

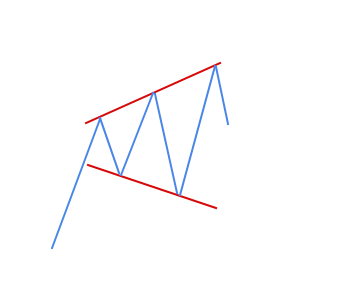
Фигура технического анализа Расходящийся треугольник

Смысл расходящегося треугольника в том, чтобы выкинуть из рынка не нужных попутчиков. Обычно, подобные модели очень затяжные, фигура может формироваться более 2 недель. 

Очень не удобная для торговли, потому что заранее не ясно, что это, формируется расходящийся треугольник или начинается новый тренд, а стопы то ставить надо. В большинстве случаев, стопы ставятся за ближайший Hi или Low, и конечно же, очередным движением их сносят.

В большинстве случаев, расходящийся треугольник действительно является фигурой разворота тренда.